&esp;&esp;87_87010计侨心中无数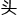羊驼驼飞奔而过，居然被无恤算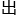来了！还算对了！

&esp;&esp;“这么快？”

&esp;&esp;“怎么可能这么快！”

&esp;&esp;他连忙想再去细看赵无恤演算的那些奇异符号和竖式，却见赵无恤脚一动，将它们统统抹去！

&esp;&esp;计侨心疼得直捂肚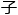，他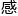觉自己已经接近了一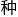前所未有的算法技巧，一旦學得，将开启数科新的时代！

&esp;&esp;也许，古算经中所记述的，“夫天可不阶而升，地不可得尺寸而度”的经天纬地之术，就不再会是传说！

&esp;&esp;他立刻换上了笑脸讨好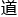：“小君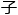不要胡闹，快将这算法说与我听听。”

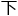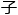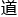&esp;&esp;赵无恤却偏要为难他一：“先生已经考校过小了，不知小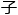能不能考校考校先生？”

&esp;&esp;“这个……”

&esp;&esp;“若是先生能答上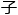小的题目，小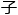定将这新颖算法拱手献上，毫不保留。”

&esp;&esp;计侨对筹算之术引以为傲，放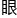晋国没有多少敌手，少有算题能将他难住，于是他今天脾气也上来了，稀里糊涂地就答应了赵无恤的挑战。

&esp;&esp;赵无恤在沙盘上画了个圆，中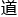：“圆，一中同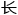也，这圆的直径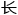一尺，周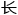未知，先生能求得此圆的确面积是多少么？”

&esp;&esp;计侨看罢，气呼呼地回答：“算经有载，周三径一，周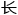是直径的三倍，而半周半径相乘得积步，如此简单的问题，小君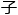是在小觑我么？”

&esp;&esp;赵无恤摸了摸无须的嘿嘿笑：“先生啊先生，枉你被称为赵氏算學第一，你觉得所谓周三径一真的准确么？”

&esp;&esp;计侨心中突突直，看赵无恤的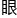神顿时就不一样了，周三径一是此时计算圆面积的普遍算法，实际上却有很大偏差，这也是困扰诸多算學专家和制车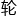、陶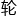工匠的大难题。

&esp;&esp;但其中的奥妙，也只有他这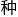数科大神能得窥一二。用“周三径一”计算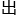来的圆周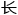，实际上不是圆的周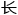而是圆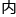接正六边形的周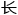，其数值要比实际的圆周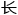小得多。

&esp;&esp;但那个神秘的比例到底如何求得，这是自从计侨八岁學数科以来，一直苦思不得其解的问题。

&esp;&esp;“请小君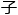教我！”对于计侨来说，什么师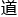尊严，都没有追求数科真理重要，他只差跪地稽首了！

&esp;&esp;赵无恤也不再难为他，继续在地上画画：“先生请看，如果我们可以在圆接正六边形把圆周等分为六条弧的基础上，再继续等分，把每段弧再分割为二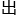，一个圆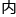接正十二边形，这个正十二边形的周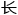不就要比正六边形的周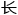更接近圆周了吗？”

&esp;&esp;“所以，如果把圆周分割得细，误差就越少，其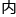接正多边形的周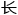就越是接近圆周。如此不断地分割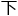去，一直到圆周无法再分割为止，它的周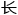就与圆周几乎完全一致了！”

&esp;&esp;计侨如同一个小學蒙童般，听得如痴如醉，不住地，心中直叹赵无恤才是真正的算學天才，竟然能想到如此巧妙的方法。

&esp;&esp;可恨自己刚才还想用那“简单”的题难住他，还想指他……真是，真是羞愧难当啊，计侨只想找个地钻去。

&esp;&esp;赵无恤展示的，其实就是割圆术，后世初中生都会的东西……但在此时，这个理论还得经过七百多年的发展，到魏晋时期才会被刘徵、祖冲之等人发现。欧洲人则要早一些，大科學家阿基米德在两百年后得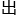了相近的结果，但要确到小数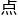后六位数，就得等到十六、十七世纪了。

&esp;&esp;所以，计侨这位秋数學家要能知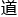，那才有鬼。

&esp;&esp;放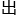了这个跨时代的理论后，赵无恤拍拍手就跑了。验证的事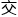，给计侨去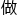吧，就让他慢慢割圆割上个三四千边形，无恤才不会那么简单就

本章尚未读完,请击一页继续阅读---->>>