
 繁体
繁体
第四百八十一章 程氏虚dian(1/2)
热门小说推荐
最近更新小说
&esp;&esp;481章
&esp;&esp;程诺从上午九 ,一直运算到第二天的凌晨两
,一直运算到第二天的凌晨两 多。
多。
&esp;&esp;期间,他一直呆在办公室里,连饭都没吃。
&esp;&esp;因为他担心一旦分心,那好不容易被他抓住的灵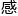 就会迅速溜掉。
就会迅速溜掉。
&esp;&esp;研究所里,只有他这一间办公室的灯还亮着。
&esp;&esp;打了个哈欠,程诺舒展了一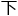

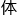 ,起
,起 泡了杯咖啡。
泡了杯咖啡。
&esp;&esp;然后他一边小 喝着,一边来欣赏他这个偶然中的发现的“伟大杰作”。
喝着,一边来欣赏他这个偶然中的发现的“伟大杰作”。
&esp;&esp;到现在,程诺还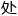 于一
于一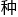 不真切的
不真切的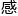 觉当中。
觉当中。
&esp;&esp;因为,这个发现,即便是以他的挑剔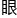 光来看,都可以称得上是“里程碑式”的意义。
光来看,都可以称得上是“里程碑式”的意义。
&esp;&esp;他敢保证,一旦将这个发现公布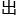 去,足以让世界上的数学家们为之疯狂。
去,足以让世界上的数学家们为之疯狂。
&esp;&esp;而这一切,都来源于一个巧合。
&esp;&esp;上午,程诺在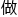 莫代尔
莫代尔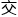 换群的同余数和无穷阶曲线上
换群的同余数和无穷阶曲线上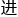 行相
行相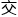 ,有理
,有理 如何
如何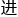 行表示的推导。
行表示的推导。
&esp;&esp;当他将无穷曲线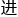 行虚
行虚 投像的时候,觉得这样算
投像的时候,觉得这样算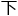 去有些太过于麻烦,便想着是否能够将所有的无穷阶曲线构成一个曲面,再去求它的一个虚
去有些太过于麻烦,便想着是否能够将所有的无穷阶曲线构成一个曲面,再去求它的一个虚 图像。
图像。
&esp;&esp;因此,当程诺把半曲面的二次虚 的图像全
的图像全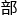 在草稿纸上画
在草稿纸上画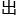 来后,对数字无比
来后,对数字无比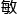
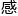 的他发现了一个有趣的现象。
的他发现了一个有趣的现象。
&esp;&esp;这些虚 ,其
,其 度可以描述曲线函数的导数。
度可以描述曲线函数的导数。
&esp;&esp;同时,可以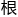 据这个虚
据这个虚 ,确定无穷阶曲线上有理
,确定无穷阶曲线上有理 位置。
位置。
&esp;&esp;程诺并没有放弃这个偶然的发现。
&esp;&esp;用了一整天的时间,程诺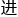 行演算,最终确定,这些经过半曲面映
行演算,最终确定,这些经过半曲面映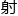
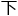 来的虚
来的虚 ,可以用于在每个正整数n的曲线上构建有理
,可以用于在每个正整数n的曲线上构建有理 ,并且这些
,并且这些 的
的 度是模块形式的权重3/2的系数。
度是模块形式的权重3/2的系数。
&esp;&esp;程诺之所以把这个虚 称之为“里程碑”式的发现,就是因为它的这两个
称之为“里程碑”式的发现,就是因为它的这两个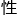 质。
质。
&esp;&esp;无穷阶曲线上有理 的构建,一直是数学界存在的几大难题之一。
的构建,一直是数学界存在的几大难题之一。
&esp;&esp;截止到现在,数学界仍未有一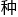 通用的简单方便方法,迅速的求
通用的简单方便方法,迅速的求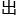 任意无穷阶曲线上有理
任意无穷阶曲线上有理 的位置,并
的位置,并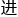 行表述。
行表述。
&esp;&esp;而这个虚 的
的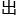 现,可以很轻易的改变这
现,可以很轻易的改变这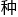 现状。
现状。
&esp;&esp;另外,这个投影虚 还可以表示模数形式权重的系数,可用于各
还可以表示模数形式权重的系数,可用于各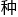 系统的构建。
系统的构建。
&esp;&esp;即便是程诺这样见过无数大风大浪的数学家,在看到这个虚 真正展现在他
真正展现在他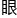 前的时候,也是无比的震撼。
前的时候,也是无比的震撼。
&esp;&esp;另外,还有欣喜。
&esp;&esp;他没想到,在攻克bsd猜想的时候,会偶然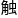 发这个大福利。
发这个大福利。
&esp;&esp;程诺暂时把这个虚 命名为程氏虚
命名为程氏虚 ,然后合上电脑,踏着朦胧的月
,然后合上电脑,踏着朦胧的月 回到公寓。
回到公寓。
&esp;&esp;即便
 上很是疲惫,但心
上很是疲惫,但心 激动的他在床上辗转反侧到后半夜才睡着。
激动的他在床上辗转反侧到后半夜才睡着。
&esp;&esp;…………
&esp;&esp;次日,程诺 着黑
着黑 圈来到研究所。
圈来到研究所。
&esp;&esp;“程教授早!”
&esp;&esp;“嗯,早。”
&esp;&esp;“程教授,你可要注意休息啊,拼是好事,但也别玩命拼。在年轻的时候就染上一 的病,老了后悔都来不及!”
的病,老了后悔都来不及!”
&esp;&esp;“周教授,谢谢你的提醒,我会注意的。”
&esp;&esp;一路打着
本章尚未读完,请 击
击 一页继续阅读---->>>
一页继续阅读---->>>
Loading...
内容未加载完成,请尝试【刷新网页】or【设置-关闭小说模式】or【设置-关闭广告屏蔽】~
推荐使用【UC浏览器】or【火狐浏览器】or【百度极速版】打开并收藏网址!
收藏网址:https://www.zhuishula.net